|
|
|
|
Translation ( notion)(coordonnées
et déplacement) |
|
|
Informations sur : Les principales façons de repérer un point |
|
|
Repérage d’un
point dans un repère
cartésien ou non cartésien (exemples) |
|
|
Info : Projection d'un point sur une droite |
|
|
Info : Projection d'un point sur eux droites sécantes |
|
|
Info : Les repères cartésiens |
|
|
Informations sur " repérage " |
Environnement du dossier:
|
|
|
|
|
|
DOSSIER : REPERAGE et COORDONNEES D
' UN POINT DANS UN REPERE CARTESIEN. |
|
|
|
|
|
|
|
1° ) Dans un repère
orthonormé . (applications ) |
|
|
|
2°) Dans un repère non - normé.( avec « x » et « y »
positifs ou nuls) |
|
|
|
|
|
|
|
|
Travaux auto
formatifs et devoir formatif |
|
A
faire : |
|||
|
TEST |
COURS |
|
|||||
|
|
|
|
|
|
|
COURS
|
|
|
|
|
|
|
|
|
|
1°) Repérage d'un point dans un repère cartésien orthonormé : Le repère
« cartésien » est constitué par l’intersection de deux droites orientées et graduées appelées « axe », ces
droites sont perpendiculaires ( ortho. ) et
« normé » parce que la
longueur des deux segments unitaires
est de la même mesure sur les deux droites sécantes , d(O,I) = d (O,J) = 1 . |
|
|
|
|
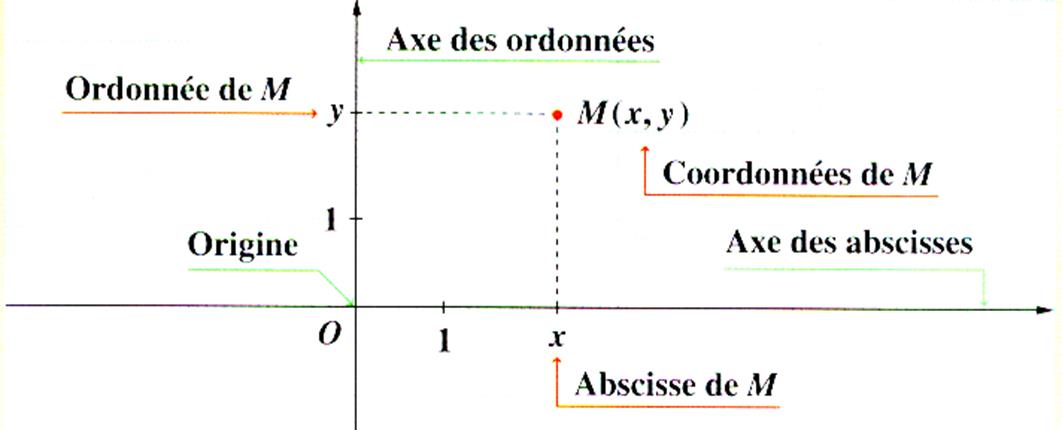
L' Axe : il
s'appelle "axe des abscisses" , L' Axe : il s'appelle : axe des ordonnées
. OI et OJ
sont les segments unitaires; ils donnent l'unité de graduation. Ils sont de même longueur: on dit "normés". |
|
|
|
|
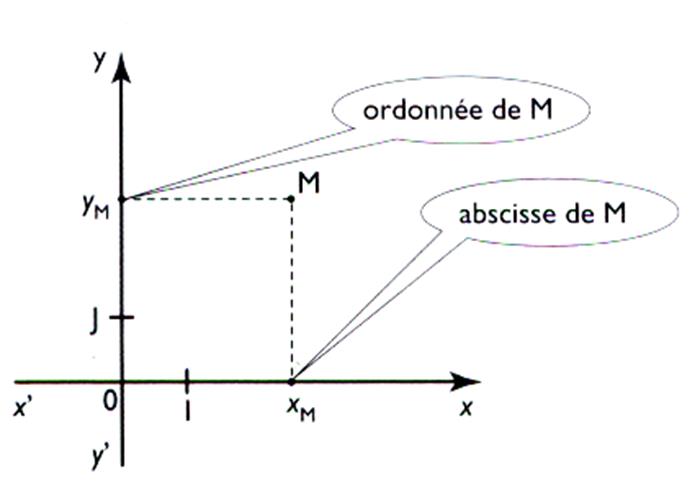
En résumé : Dans un repère ( O , I , J )
du plan , d'axes ( x' O x ) et ( y' O y ) perpendiculaires , chaque
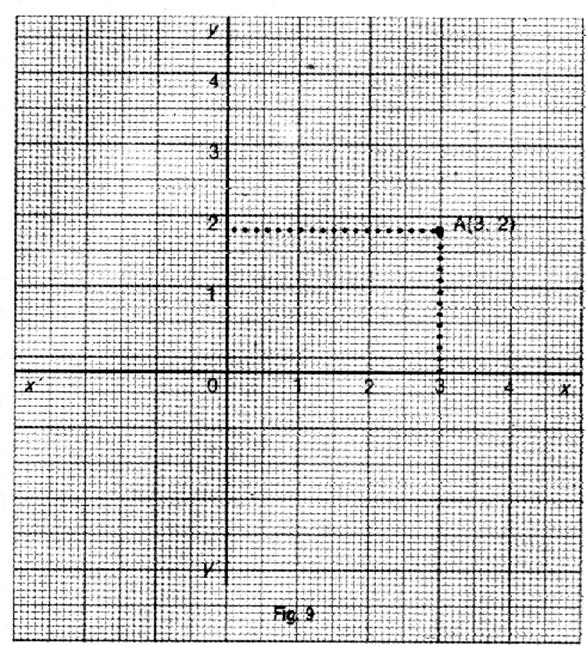
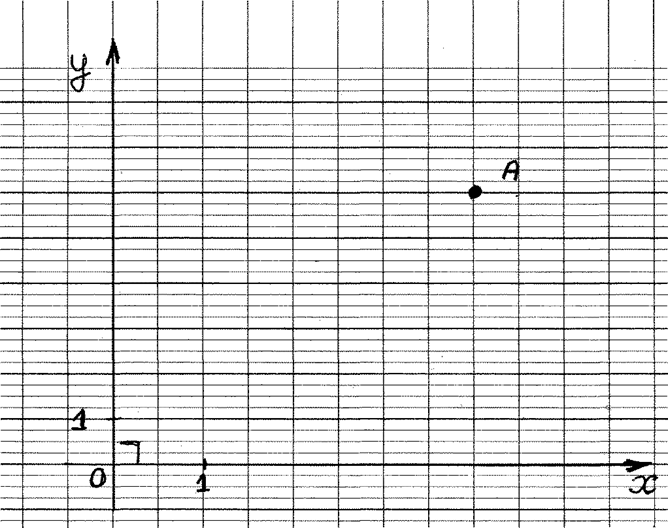
point est repéré par ses coordonnées : son abscisse xM et son ordonnée yM . On écrit : M ( xM ; y M) Application : on recherche des coordonnées du point A |
|
|
|
|
Les coordonnées
du point A dans le repère orthonormé est ( 3;2). |
|
|
|
|
|
|
|
|
|
1°) Coordonnées du point « A » dans le repère cartésien
orthonormé : Coordonnées du point : A.(
x A ; YA )
; exemple : A ( 3 ; 2 ) Les coordonnées d’ un point sont données par
deux valeurs numériques données dans
un ordre à respecter : la première valeur est appelée
« abscisse » ; la seconde valeur est appelée
« ordonné » . Pour
déterminer la position d ’ un point dans un
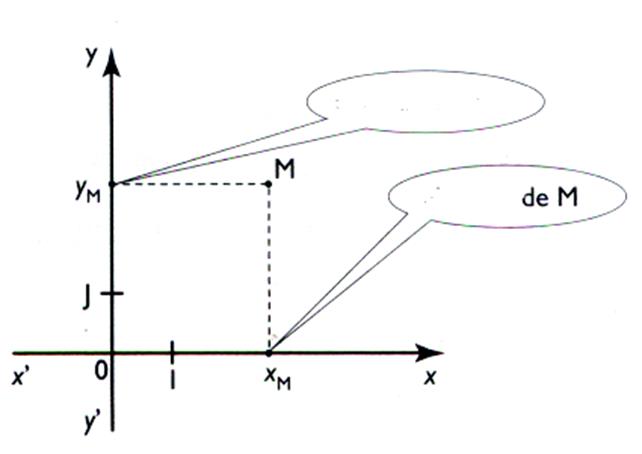
repère cartésien il faut deux nombres : Ces deux nombres .( x (M) ; y (M) ) sont appelés :
coordonnées du « point » M
Le premier nombre correspond à la position du projeté du
point « M » (noté : . x M ) sur l ’
« axe x’ x » ; appelé « axe des abscisses » Le second nombre correspond à la position du projeté du point
« M » .(noté Y(M) ) sur l ’ « axe y
’y » ; appelé « axe
des ordonnées » |
|
|
|
|
|
|
|
|
|
Procédure permettant de trouver les coordonnées d ’
un point dans un plan :
Pour trouver les coordonnées d’un point dans un plan : « on projète
l’image du point sur les deux axes » Il faut tracer une
droite parallèle à l ’ axe des ordonnées (y’y) pour trouver la valeur de l ’ abscisse et une autre
droite parallèle à l ’ axe des abscisses (x’x) pour trouver la valeur de l ‘ordonnée. 2°)
Repérage d'un point dans un repère cartésien ortho - non normé : Le repère « cartésien » est
constitué par l’intersection de deux droites orientées et graduées
appelées « axe », ces droites
sont perpendiculaires
( ortho. ) et « non - normé »parce
que la longueur des deux segments
unitaires ne sont pas de la même
mesure sur les deux droites sécantes ,
d(O,I)
¹ d (O,J) Exemple de repère "non - normé " ayant
pour segment unitaire OI = 1
et pour OJ = 0,1 : |
|
|
|
|
|
|
|
|
|
Activité 1: Données :
Un véhicule parcours On a mis ses données dans un tableau : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vitesse en Km/h |
20 |
40 |
60 |
80 |
100 |
120 |
|
Distance (m) |
20 |
40 |
80 |
140 |
220 |
320 |
|
|
|
|
|
|
|
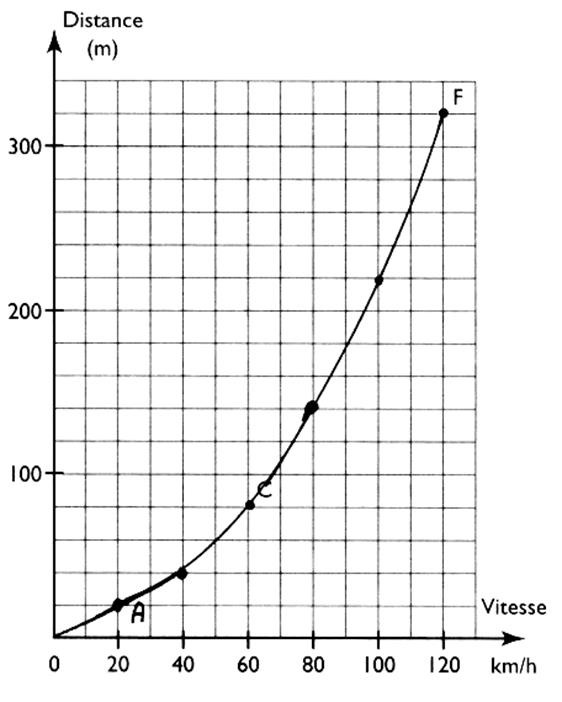
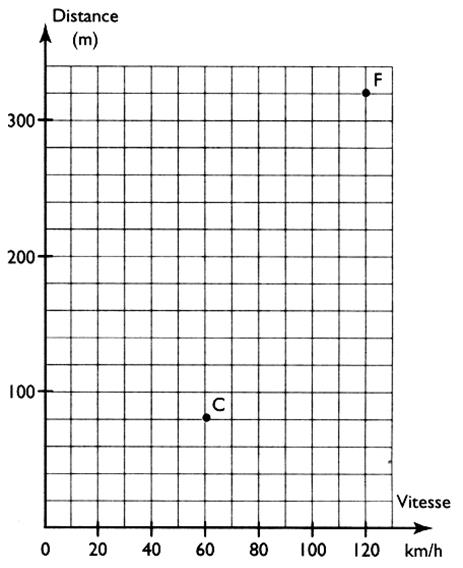
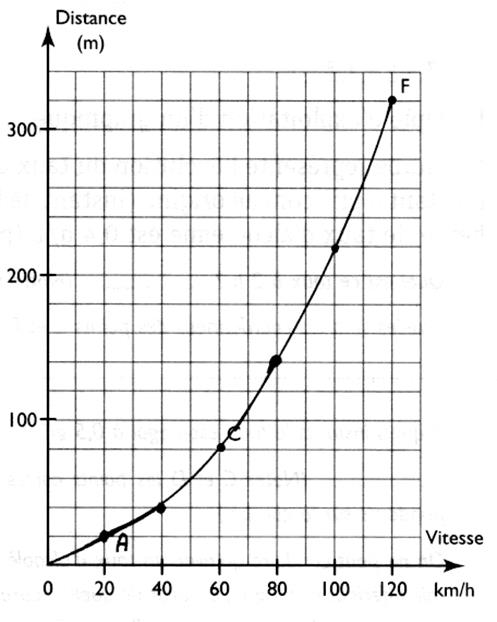
On veut représenter graphiquement les données d'un tableau : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Remarquer que les graduations : sur
"x" : [0;100 ]
= 10 carreaux ; Pour Et sur "y" : [ 0;100] = 5
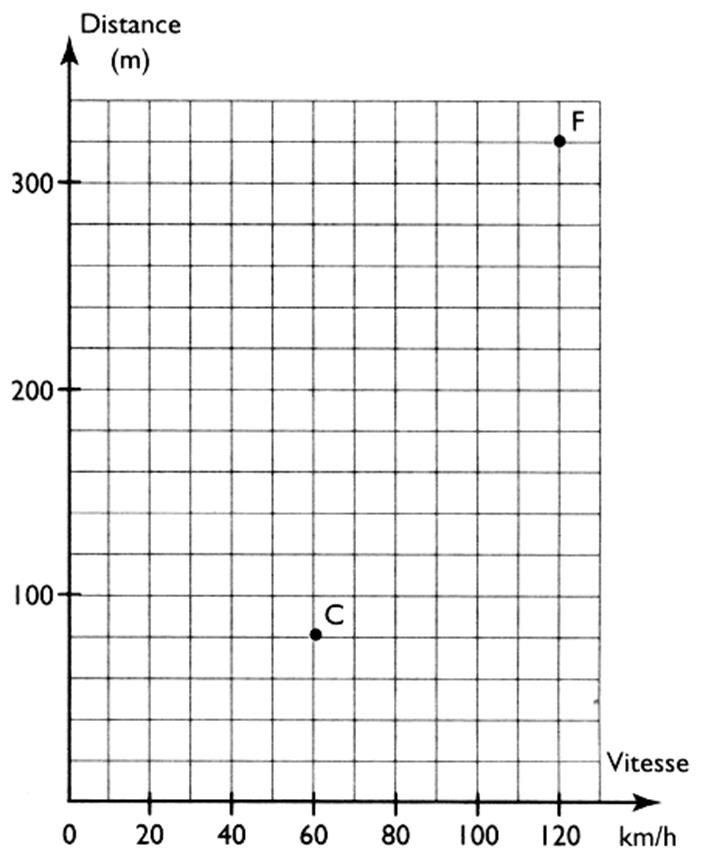
carreaux ;pour Activité 2 : Recherche des coordonnées d'un point
dans un repère: A partir d'un point
donné ( ou choisi ) on trace des droites parallèles
aux axes. Le point F correspond à la vitesse de On écrit : F ( 120 ; 320
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Il en est de même pour le point C : C ( 60;80) |
|
|
|
|
Activité suivante : Exploitation du graphique . |
|
|
|
|
|
|
|
|
|
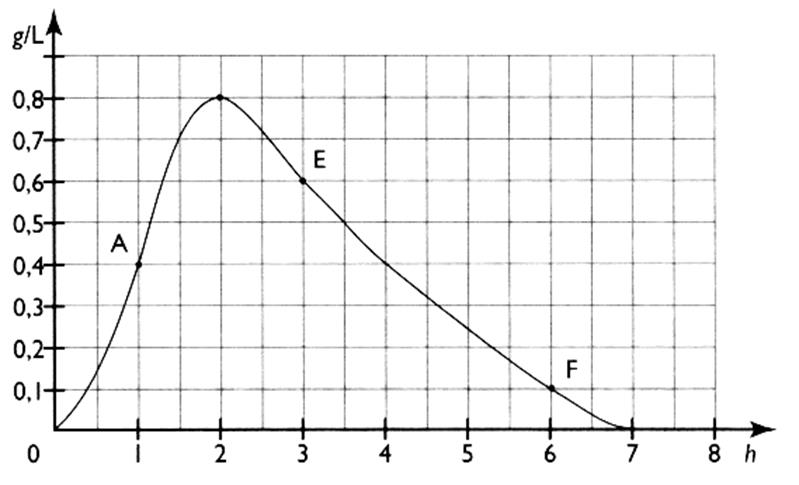
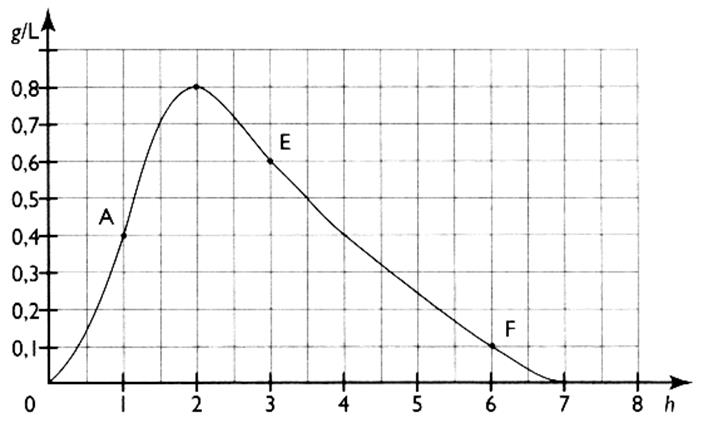
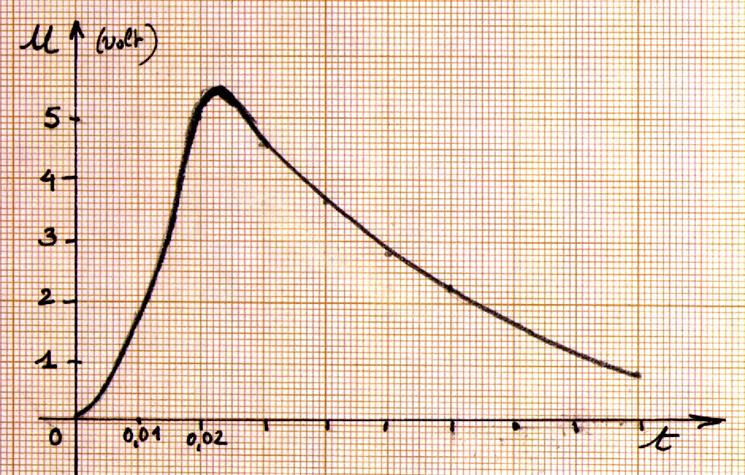
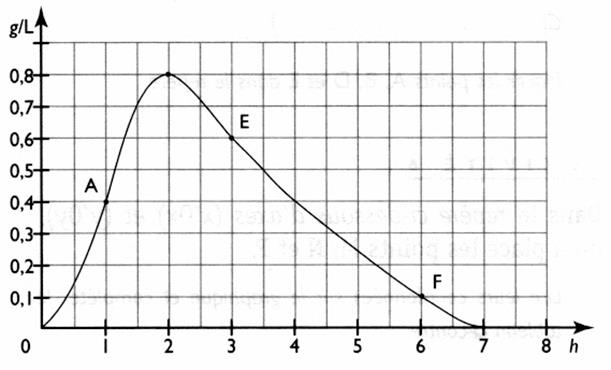
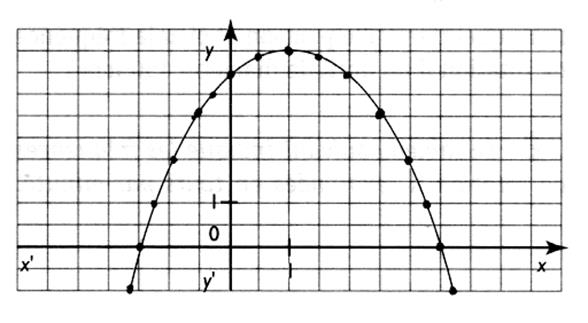
La courbe représente l'évolution du taux d'alcoolémie ( en g /L ) en fonction du temps , à partir de l'instant 0
pris comme origine ( instant de la consommation de deux verres de vin). Analyse de la courbe : Au bout d'une heure
, le taux d'alcoolémie est
0,4 g/L ( point A sur la courbe ) A 1,5 h le taux est de 0,5 g/L ( pt. A) Au bout de 2 heures le taux est maximum , il
est de Au bout de 3 heures le taux a baissé
à Au bout de 6 heures ce taux est de 0,1 g/L ( pt . F ) Ce taux est égal à 0 au bout de
7 heures . Commentaire : on ne peut conduire qu'avec un taux inférieur à 0,5 g/L
; Le taux est progresse et est égal à 0,5
g/L à
de 1,2 h , le taux baisse pour revenir à 0,5 g/L au bout de 3,5 h . Conclusion : On prendra la route tranquillement 3 ,5 h après avoir consommé. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TRAVAUX AUTO FORMATIFS. |
|
|
|
|
|
|
|
|
|
Pré requis : |
|
|
|
|
Evaluation : |
|
|
|
|
Série 1 : |
|
|
|
|
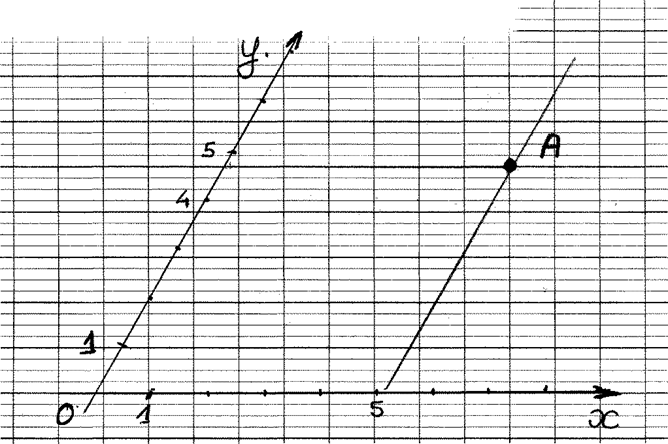
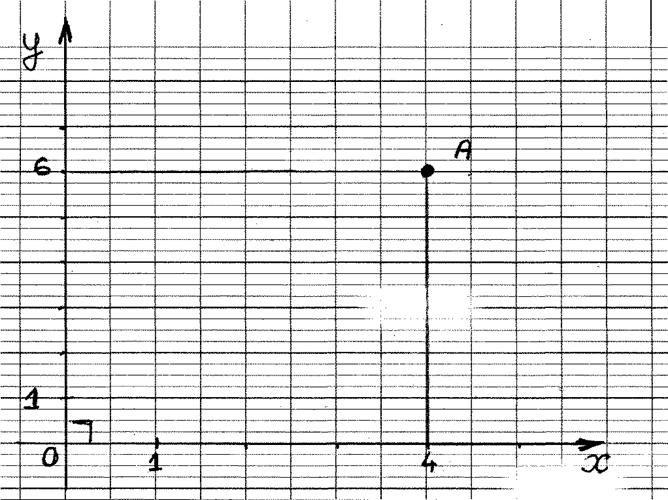
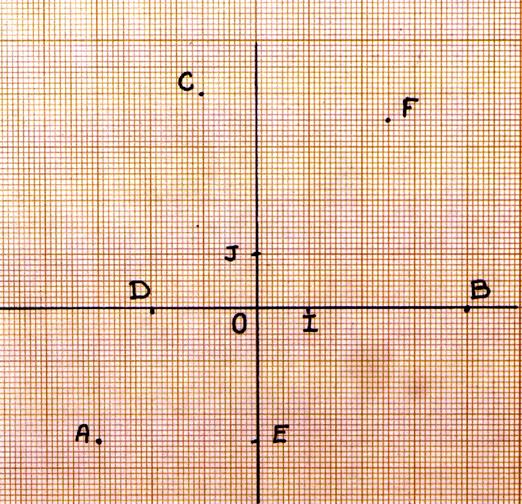
Donnez les coordonnées du point « A » . |
|
|
|
|
|
|
|
|
|
A ( ….. ; ……) |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
A ( ….. ; ……) |
|
|
|
|
|
|
|
|
|
A ( ….. ; ……) |
|
|
|
|
|
|
|
|
|
A ( ….. ; ……) |
|
|
|
|
|
|
|
|
|
Série
2 : |
|
|
|
|
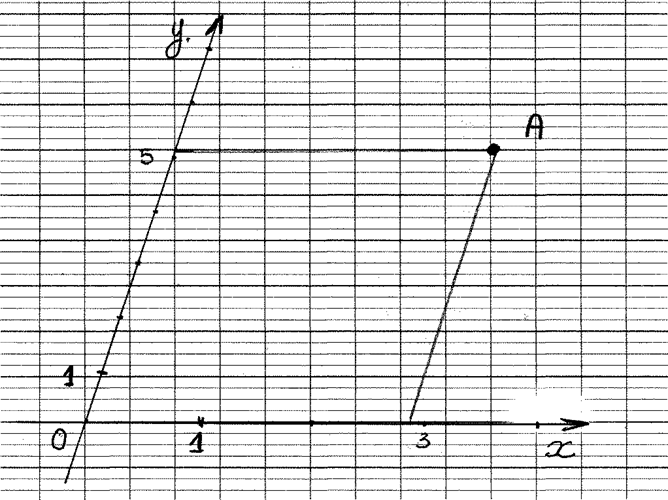
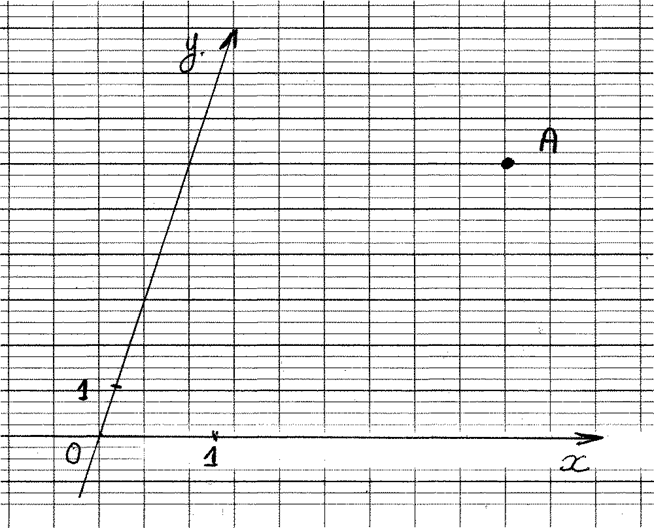
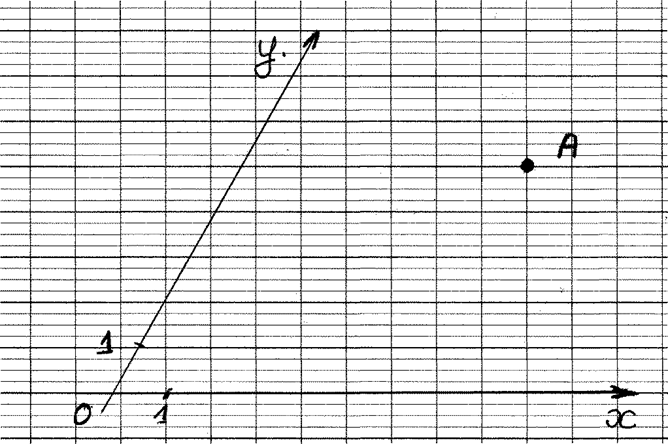
1°) Graduez les repères cartésiens . 2°) Donnez les coordonnées du point « A » |
|
|
|
|
|
|
|
|
|
A ( ….. ; ……) |
|
|
|
|
|
|
|
|
|
A ( ….. ; ……) |
|
|
|
|
|
|
|
|
|
A ( ….. ; ……) |
|
|
|
|
|
|
|
|
|
CONTROLE: |
|
|
|
|
Compléter
le dessin : Dites tout ce que vous
savez sur l'image ci
dessous . |
|
|
|
|
|
|
|
|
|
v Qu ‘ appelle -t - on « coordonnées d’un
point » ? v Comment appelle t - on
l’axe des « x » ? v Axes des abscisses
v Comment appelle t - on
l’axe des « y » ? Axes des ordonnées
v Sur quel « axe » trouve t - on les
« ordonnées » ? l’axe des « y » v Sur quel « axe » trouve t - on les
« abscisses » ? l’axe des « x » v Donner la procédure à utiliser pour trouver les
coordonnées d ’ un point dans un repère orthonormé. v Procédure permettant de trouver les coordonnées d ’ un point dans un plan : v Pour trouver les coordonnées d’un point dans un
plan : v « on projète
l’image du point sur les deux axes » v Il faut tracer une droite parallèle à l ’ axe des
ordonnées (y’y) pour trouver la
valeur de l ’ abscisse et une autre droite parallèle à l ’ axe des abscisses
(x’x) pour
trouver la valeur de l ‘ordonnée. |
|
|
|
|
|
|
|
|
|
EVALUATION : |
|
|
|
|
|
|
|
|
|
:Voir Contrôle Continu Fiche
situation @ 5 1°) Dans un
repère ( O , 2°)Travail : citer dix
couples de décimaux positifs au plus |
|
|
SUJET 3
|
TC2 |
E |
T |
C |
|
Repérage d’un point dans un plan
(P) muni d’un repère orthogonal ( O,I, J ) |
|
|
|
|